�x�N�g����͂Ŏg�p�����R�[�h�S��
�T�e���C�g�T�C�g�g�悭�킩��x�N�g������h�Ŏg�p����LaTeX�R�[�h�ł��B
���̂܂܃R�s�y���č쐬�ł��܂��B
�Ȃ��ȉ��̃T�C�g�l�A
�ɂ����āA�R�[�h�����̂܂܃R�s�y����ΊȒP�ɐ����摜���쐬����܂��B
��{�I�Ɍ����Ƃ��Ďg������̂�I�����čڂ��Ă���̂Ŋw�K�p��Web�T�C�g�쐬�p�Ȃǂɂ��]�p�ł���ł��傤�B
�������摜��R�[�h�����p����ꍇ���Ǘ��l�̋��͂���܂��o�b�N�����N��Љ�Ȃǂ̐����͕K�����肢���܂��B
�X�J���[�O�d�ό���
\begin{eqnarray*}
{\bf A}\;\cdot\;\left({\bf B}\;\times\;{\bf C}\right)\quad=\quad
\left|
\begin{array}{ccc}
A_x & A_y & A_z\\
B_x & B_y & B_z\\
C_x & C_y & C_z
\end{array}
\right|
\end{eqnarray*}
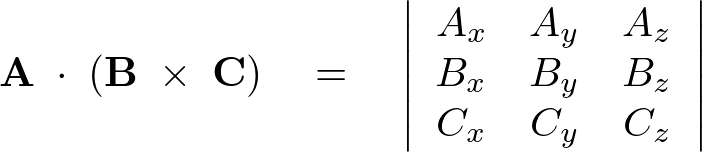
�s�W�J�@����
\[
\left|
\begin{array}{lcr}
a_1 & b_1 & c_1\\
a_2 & b_2 & c_2\\
a_3 & b_3 & c_3
\end{array}
\right|
=a_1
\left|
\begin{array}{lr}
b_2 & c_2\\
b_3 & c_3
\end{array}
\right|
-a_2
\left|
\begin{array}{lr}
b_1 & c_1\\
b_3 & c_3
\end{array}
\right|
+a_3
\left|
\begin{array}{lr}
b_1 & c_1\\
b_2 & c_2
\end{array}
\right|
\]
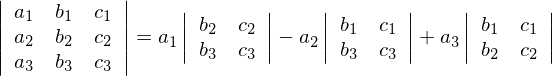
\[
\left|
\begin{array}{lcr}
+ & - & +\\
- & + & -\\
+ & - & +
\end{array}
\right|
\]
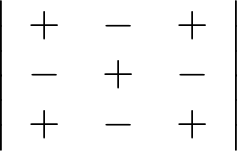
\[
\left|
\begin{array}{lcr}
A_x & A_y & A_z\\
B_x & B_y & B_z\\
C_x & C_y & C_z
\end{array}
\right|
\]
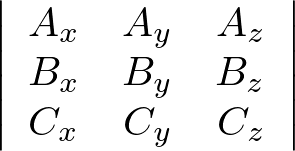
\begin{eqnarray*}
\left|
\begin{array}{lcr}
A_x & B_x & C_x\\
A_y & B_y & C_y\\
A_z & B_z & C_z
\end{array}
\right|
\;&=&\;
A_x
\left|
\begin{array}{cc}
B_y & C_y\\
B_z & C_z
\end{array}
\right|
\quad-\quad
A_y
\left|
\begin{array}{cc}
B_x & C_x\\
B_z & C_z
\end{array}
\right|
\quad+\quad
A_z
\left|
\begin{array}{cc}
B_x & C_x\\
B_y & C_y
\end{array}
\right|\nonumber\\
\nonumber\\
=\;A_x(B_yC_z\quad&-&\quad B_zC_y)\quad-\quad A_y(B_xC_z\quad-\quad B_zC_x)
\quad+\quad A_z(B_xC_y\quad-\quad B_yC_x)\nonumber\\
\nonumber\\
=\;A_x(B_yC_z\quad&-&\quad B_zC_y)\quad+\quad A_y(B_zC_x\quad-\quad B_xC_z)
\quad+\quad A_z(B_xC_y\quad-\quad B_yC_x)\nonumber\\
\end{eqnarray*}
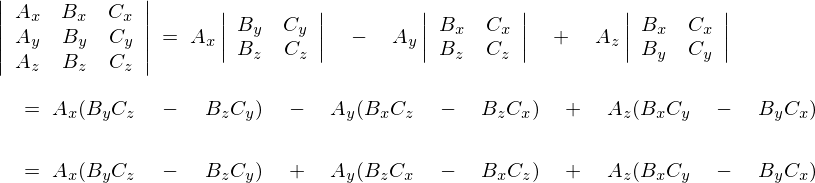
\begin{eqnarray*}
\left|
\begin{array}{lcr}
A_x & A_y & A_z\\
B_x & B_y & B_z\\
C_x & C_y & C_z
\end{array}
\right|
=A_x(B_yC_z\quad-\quad B_zC_y)\quad+\quad A_y(B_zC_x\quad-\quad B_xC_z)
\quad+\quad A_z(B_xC_y\quad-\quad B_yC_x)
\end{eqnarray*}
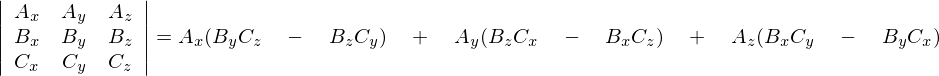
\begin{eqnarray*}
\left|
\begin{array}{lcr}
A_x & A_y & A_z\\
B_x & B_y & B_z\\
C_x & C_y & C_z
\end{array}
\right|
={\bf A}\;\cdot\;\left({\bf B}\;\times\;{\bf C}\right)
\end{eqnarray*}
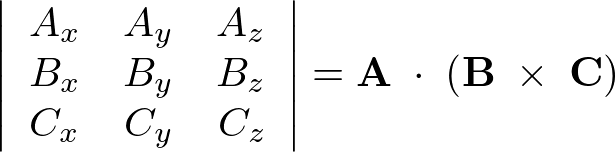
\begin{eqnarray*}
{\bf A}\cdot\left({\bf B}\;\times\;{\bf C}\right)\;=\;{\bf B}\cdot\left({\bf C}\;\times\;{\bf A}\right)\;=\;{\bf C}\cdot\left({\bf A}\;\times\;{\bf B}\right)
\end{eqnarray*}
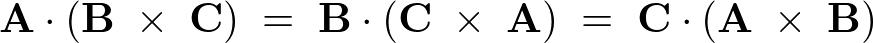
�x�N�g���O�d��
\[
{\bf A}\;\times\;\left({\bf B}\;\times\;{\bf C}\right)\;=\;\left({\bf A}\;\cdot\;{\bf C}\right)\;{\bf B}\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)\;{\bf C}
\]
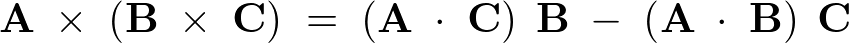
\[
{\bf A}\;\times\;\left({\bf B}\;\times\;{\bf C}\right)\;=\;{\bf A}\;\times\;{\bf D}
\]
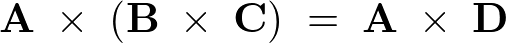
\begin{eqnarray*}
{\bf A}\;\times\;\left({\bf B}\;\times\;{\bf C}\right)\;&=&\;{\bf A}\;\times\;{\bf D}\nonumber\\
&=&\;\underbrace{\left(A_yD_z\;-\;A_zD_y\right)}{\bf i}\;+\;\underbrace{\left(A_zD_x\;-\;A_xD_z\right)}{\bf j}\;+\;\underbrace{\left(A_xD_y\;-\;A_yD_x\right)}{\bf k}\nonumber\\
&&\:\:\qquad\quad (1) \quad\qquad\qquad\qquad\quad\;\; (2) \;\;\;\qquad\qquad\qquad\qquad (3)\nonumber\\
\end{eqnarray*}
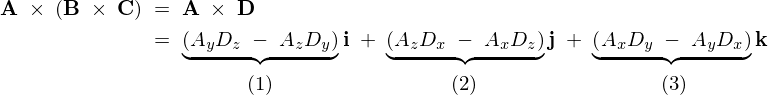
\begin{eqnarray*}
(1)\;=\;A_y\underbrace{\left(B_xC_y\;-\;B_yC_x\right)}\;-\;A_z\underbrace{\left(B_zC_x\;-\;B_xC_z\right)}\;=\;A_yB_xC_y\;-\;A_yB_yC_x\;-\;A_zB_zC_x\;+\;A_zB_xC_z\nonumber\\
D_z\;\qquad\qquad\qquad\quad\qquad D_y\;\quad\qquad\;=\;\left(A_yC_y\;+\;A_zC_z\right)B_x\;-\;\left(A_yB_y\;+\;A_zB_z\right)C_x\nonumber\\
\end{eqnarray*}
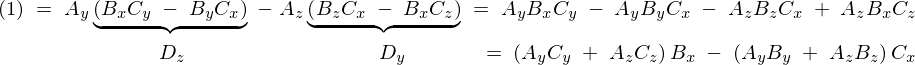
\begin{eqnarray*}
\left(A_yC_y\;+\;A_zC_z\right)B_x\;-\;\left(A_yB_y\;+\;A_zB_z\right)C_x
&=&\;\left(A_xC_x\;+\;A_yC_y\;+\;A_zC_z\right)B_x\;-\;\left(A_xB_x\;+\;A_yB_y\;+\;A_zB_z\right)C_x\nonumber\\
&=&\;\left({\bf A}\;\cdot\;{\bf C}\right)B_x\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)C_x\;\cdots\cdots\;(1)^{\prime}\nonumber\\
\end{eqnarray*}
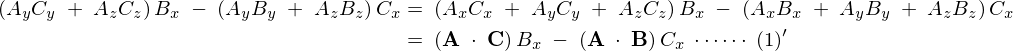
\begin{eqnarray*}
(2)\;&=&\;A_z\left(B_yC_z\;-\;B_zC_y\right)\;-\;A_x\left(B_xC_y\;-\;B_yC_x\right)\\
&=&\;A_zB_yC_z\;-\;A_zB_zC_y\;-\;A_xB_xC_y\;+\;A_xB_yC_x\nonumber\\
&=&\;\left(A_zC_z\;+\;A_xC_x\right)B_y\;-\;\left(A_zB_z\;+\;A_xB_x\right)C_y\nonumber\\
&=&\;\left(A_xC_x\;+\;A_yC_y\;+\;A_zC_z\right)B_y\;-\;\left(A_xB_x\;+\;A_yB_y\;+\;A_zB_z\right)C_y\nonumber\\
&=&\;\left({\bf A}\;\cdot\;{\bf C}\right)B_y\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)C_y\;\cdots\cdots\;(2)^{\prime}\nonumber\\
\end{eqnarray*}
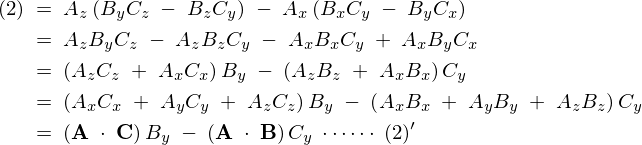
\begin{eqnarray*}
(3)\;&=&\;A_x\left(B_zC_x\;-\;B_xC_z\right)\;-\;A_y\left(B_yC_z\;-\;B_zC_y\right)\\
&=&\;A_xB_zC_x\;-\;A_xB_xC_z\;-\;A_yB_yC_z\;+\;A_yB_zC_y\nonumber\\
&=&\;\left(A_xC_x\;+\;A_yC_y\right)B_z\;-\;\left(A_xB_x\;+\;A_yB_y\right)C_z\nonumber\\
&=&\;\left(A_xC_x\;+\;A_yC_y\;+\;A_zC_z\right)B_z\;-\;\left(A_xB_x\;+\;A_yB_y\;+\;A_zB_z\right)C_z\nonumber\\
&=&\;\left({\bf A}\;\cdot\;{\bf C}\right)B_z\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)C_z\;\cdots\cdots\;(3)^{\prime}\nonumber\\
\end{eqnarray*}
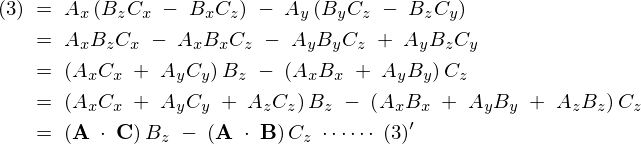
\begin{eqnarray*}
(1)^{\prime}{\bf i}\;+\;(2)^{\prime}{\bf j}\;+\;(3)^{\prime}{\bf k}\;&=&\;\left({\bf A}\;\cdot\;{\bf C}\right)B_x\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)C_x\;+\;\left({\bf A}\;\cdot\;{\bf C}\right)B_y\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)C_y\;+\;\left({\bf A}\;\cdot\;{\bf C}\right)B_z\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)C_z\nonumber\\
&=&\;\left({\bf A}\;\cdot\;{\bf C}\right)\left(B_x\;+\;B_y\;+\;B_z\right)\;-\;\left({\bf A}\;\cdot\;{\bf B}\right)\left(C_x\;+\;C_y\;+\;C_z\right)\nonumber\\
&=&\;\left({\bf A}\;\cdot\;{\bf C}\right){\bf B}\;-\;\left({\bf A}\;\cdot\;{\bf B}\right){\bf C}\nonumber\\
\end{eqnarray*}
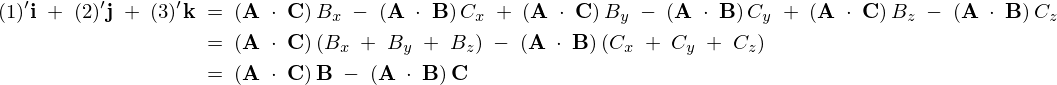
�x�N�g���̔����ϕ�
\begin{eqnarray*}
\frac{d{\bf A}(t)}{dt}\;=\;\frac{dA_x(t)}{dt}{\bf i}\;+\;\frac{dA_y(t)}{dt}{\bf j}\;+\;\frac{dA_z(t)}{dt}{\bf k}\qquad\left(\frac{{\bf A}(t)}{dt}\;=\;{\bf A}^{\prime}(t)\right)
\end{eqnarray*}
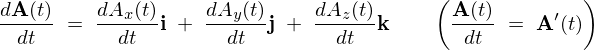
\begin{eqnarray*}
&(1)&\quad\frac{d{\bf \kappa}}{dt}\;=\;{\bf 0}\qquad\qquad\qquad\qquad(2)\quad\frac{d}{dt}\left(C{\bf A}(t)\right)\;=\;C\frac{d{\bf A}(t)}{dt}\nonumber\\
&(3)&\quad\frac{d}{dt}\left({\bf A}(t)\;+\;{\bf B}(t)\right)\;=\;\frac{d{\bf A}(t)}{dt}\;+\;\frac{d{\bf B}(t)}{dt}\nonumber\\
&(4)&\quad\frac{d}{dt}\left({\bf A}(t)\cdot{\bf B}(t)\right)\;=\;\frac{d{\bf A}(t)}{dt}\cdot{\bf B}(t)\;+\;{\bf A}(t)\cdot\frac{d{\bf B}(t)}{dt}\nonumber\\
&(5)&\quad\frac{d}{dt}\left({\bf A}(t)\;\times\;{\bf B}(t)\right)\;=\;\frac{d{\bf A}(t)}{dt}\;\times\;{\bf B}(t)\;+\;{\bf A}(t)\;\times\;\frac{d{\bf B}(t)}{dt}\nonumber\\
\end{eqnarray*}
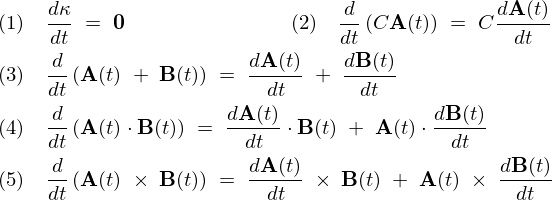
\begin{eqnarray*}
\frac{d}{dt}\left({\bf A}(t)\cdot{\bf B}(t)\right)\;&=&\;\frac{d{\bf A}(t)}{dt}{\bf B}(t)\;+\;{\bf A}(t)\frac{d{\bf B}(t)}{dt}\nonumber\\
&=&\;\left(\frac{dA_x(t)}{dt}{\bf i}\;+\;\frac{dA_y(t)}{dt}{\bf j}\;+\;\frac{dA_z(t)}{dt}{\bf k}\right)\cdot\Big(B_x(t){\bf i}\;+\;B_y(t){\bf j}\;+\;B_z(t){\bf k}\Big)\nonumber\\
&&+\;\Big(A_x(t){\bf i}\;+\;A_y(t){\bf j}\;+\;A_z(t){\bf k}\Big)\cdot\left(\frac{dB_x(t)}{dt}{\bf i}\;+\;\frac{dB_y(t)}{dt}{\bf j}\;+\;\frac{dB_z(t)}{dt}{\bf k}\right)\nonumber\\
&=&\;\frac{d{\bf A}(t)}{dt}\cdot{\bf B}(t)\;+\;{\bf A}(t)\cdot\frac{d{\bf B}(t)}{dt}\nonumber\\
\end{eqnarray*}
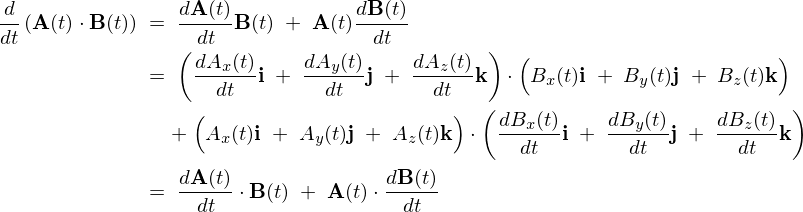
\[
\frac{d}{dt}\left({\bf A}(t)\cdot{\bf B}(t)\right)\;=\;\frac{d{\bf A}(t)}{dt}\cdot{\bf B}(t)\;+\;{\bf A}(t)\cdot\frac{d{\bf B}(t)}{dt}
\]
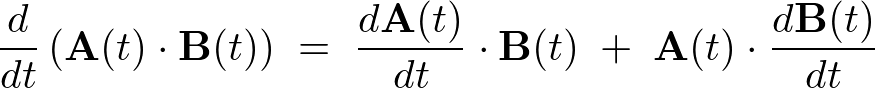
\[
\frac{d}{dt}\left({\bf A}(t)\;\times\;{\bf B}(t)\right)\;=\;\frac{d{\bf A}(t)}{dt}\;\times\;{\bf B}(t)\;+\;{\bf A}(t)\;\times\;\frac{d{\bf B}(t)}{dt}
\]
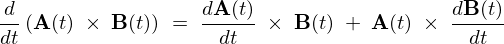
\begin{eqnarray*}
{\bf A}(t)\;\times\;{\bf B}(t)\;&=&\;\Big(A_y(t)B_z(t)\;-\;A_z(t)B_y(t)\Big){\bf i}\nonumber\\
&&\qquad\qquad+\;\Big(A_z(t)B_x(t)\;-\;A_x(t)B_z(t)\Big){\bf j}\nonumber\\
&&\qquad\qquad\qquad\qquad+\Big(A_x(t)B_y(t)\;-\;A_y(t)B_x(t)\Big){\bf k}\nonumber\\
\end{eqnarray*}
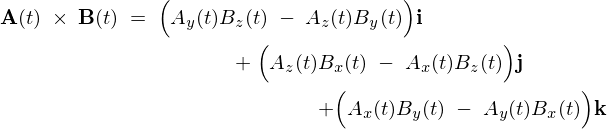
\begin{eqnarray*}
\frac{d}{dt}\left({\bf A}(t)\;\times\;{\bf B}(t)\right)\;&=&\;\left\{\left(\frac{dA_y(t)}{dt}B_z(t)\;+\;A_y(t)\frac{dB_z(t)}{dt}\right)\;-\;\left(\frac{dA_z(t)}{dt}B_y(t)\;+\;A_z(t)\frac{dB_y(t)}{dt}\right)\right\}\;{\bf i}\nonumber\\
\qquad\qquad&&\qquad+\left\{\left(\frac{dA_z(t)}{dt}B_x(t)\;+\;A_z(t)\frac{dB_x(t)}{dt}\right)\;-\;\left(\frac{dA_x(t)}{dt}B_z(t)\;+\;A_x(t)\frac{dB_z(t)}{dt}\right)\right\}\;{\bf j}\nonumber\\
\qquad\qquad\qquad\qquad&&\qquad\qquad+\left\{\left(\frac{dA_x(t)}{dt}B_y(t)\;+\;A_x(t)\frac{dB_y(t)}{dt}\right)\;-\;\left(\frac{dA_y(t)}{dt}B_x(t)\;+\;A_y(t)\frac{dB_x(t)}{dt}\right)\right\}\;{\bf k}\nonumber\\
\nonumber\\
&=&\;\underbrace{\left(\frac{dA_y(t)}{dt}B_z(t)\;-\;\frac{dA_z(t)}{dt}B_y(t)\right)\;{\bf i}\;+\;\left(\frac{dA_z(t)}{dt}B_x(t)\;-\;\frac{dA_x(t)}{dt}B_z(t)\right)\;{\bf j}\;+\;\left(\frac{dA_x(t)}{dt}B_y(t)\;-\;\frac{dA_y(t)}{dt}B_x(t)\right)\;{\bf k}\;}\nonumber\\
&&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\qquad\qquad\qquad\qquad\qquad(1)\nonumber\\
\qquad&&\qquad+\;\underbrace{\left(A_y(t)\frac{dB_z(t)}{dt}\;-\;A_z(t)\frac{dB_y(t)}{dt}\right)\;{\bf i}\;+\;\left(A_z(t)\frac{dB_x(t)}{dt}\;-\;A_x(t)\frac{dB_z(t)}{dt}\right)\;{\bf j}\;+\;\left(A_x(t)\frac{dB_y(t)}{dt}\;-\;A_y(t)\frac{dB_x(t)}{dt}\right)\;{\bf k}\;}\nonumber\\
&&\;\quad\quad\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad\qquad\qquad(2)\nonumber\\
\end{eqnarray*}
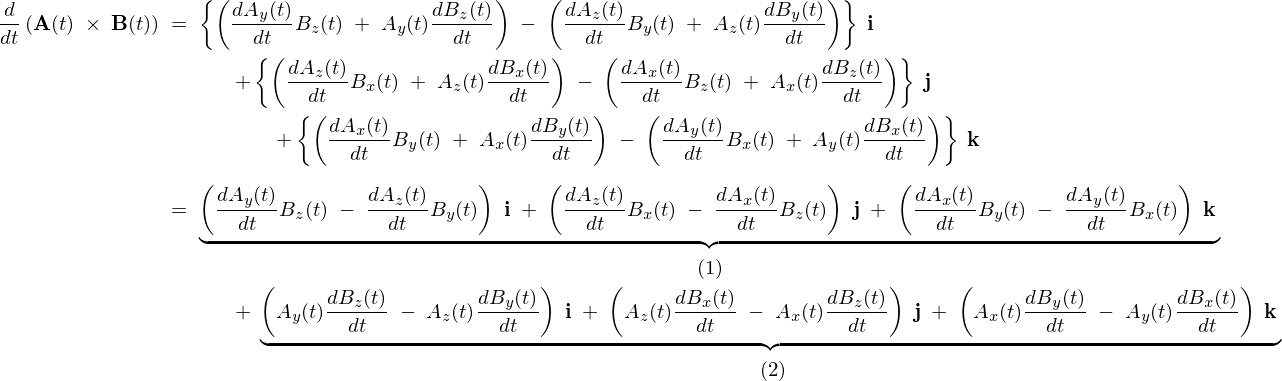
\[
(1)\;=\;\frac{d{\bf A}(t)}{dt}\;\times\;{\bf B}(t)\qquad\qquad(2)\;=\;{\bf A}(t)\;\times\;\frac{d{\bf B}}{dt}
\]

�x�N�g���̐ϕ�
\[
{\bf B}(t)\;=\;\int{\bf A}(t)dt
\]
\[
\frac{d}{dt}\left({\bf B}(t)\;+\;{\bf \kappa}\right)\;=\;{\bf A}\qquad\qquad\left(\;{\bf \kappa}\;=\;Const.\right)
\]
\[
\int{\bf A}(t)dt\;=\;{\bf B}(t)\;+\;{\bf \kappa}
\]
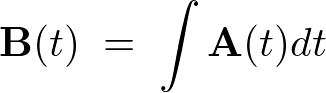
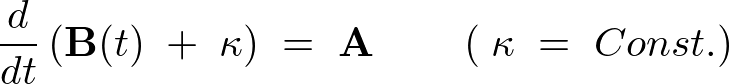
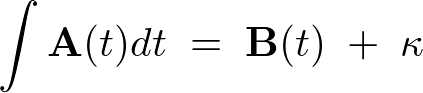
\[
\int{\bf A}(t)dt\;=\;\left(\int A_x(t)dt\right)\;{\bf i}\;+\;\left(\int A_y(t)dt\right)\;{\bf j}\;+\;\left(\int A_z(t)dt\right)\;{\bf k}
\]
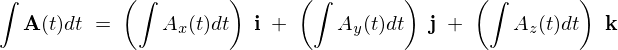
\[
\int {\bf A}(t)dt\;=\;\left(\int^{t_2}_{t_1}A_x(t)dt\right)\;{\bf i}\;+\;\left(\int^{t_2}_{t_1}A_y(t)dt\right)\;{\bf j}\;+\;\left(\int^{t_2}_{t_1}A_z(t)dt\right)\;{\bf k}
\]
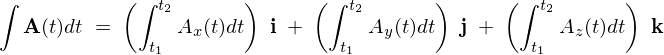
�x�N�g���s��ϕ�����
\begin{eqnarray*}
&&\int\left({\bf A}(t)\;+\;{\bf B}(t)\right)dt\;=\;\int{\bf A}(t)dt\;+\;\int{\bf B}(t)dt\\
&&\int{\bf A}(t)\;\cdot\;\frac{d{\bf B}(t)}{dt}dt\quad=\;{\bf A}(t)\;\cdot\;{\bf B}(t)\;-\;\int\frac{d{\bf A}(t)}{dt}\;\cdot\;{\bf B}(t)dt\\
&&\int{\bf A}\;\times\;\frac{d{\bf B}(t)}{dt}dt\;\quad=\;{\bf A}\;\times\;{\bf B}\;-\;\int\frac{d{\bf A}(t)}{dt}\;\times\;{\bf B}(t)dt\\
&&\int{\bf A}(t)\;\cdot\;\frac{d{\bf A}(t)}{dt}dt\quad=\;\frac{1}{2}{\bf A}(t)\;\cdot\;{\bf A}(t)\;+\;{\bf \kappa}\\
\end{eqnarray*}
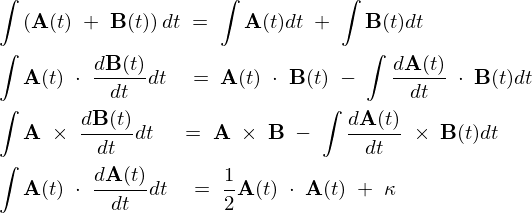
\begin{eqnarray*}
{\bf A}\;\cdot\;{\bf B}\;&=&\;\int\left(\frac{d{\bf A}(t)}{dt}\;\cdot\;{\bf B}(t)\;+\;{\bf A}(t)\;\cdot\;\frac{d{\bf B}(t)}{dt}\right)dt\;+\;{\bf \kappa}\nonumber\\
{\bf A}\;\cdot\;{\bf B}\;&=&\;\int\frac{d{\bf A}(t)}{dt}\;\cdot\;{\bf B}(t)dt\;+\;\int{\bf A}(t)\;\cdot\;\frac{d{\bf B}(t)}{dt}dt\nonumber\\
\nonumber\\
\Longrightarrow\;\int{\bf A}(t)\;&\cdot&\;\frac{d{\bf B}(t)}{dt}\;=\;{\bf A}(t)\;\cdot\;{\bf B}(t)\;-\;\int\frac{d{\bf A}(t)}{dt}\;\cdot\;{\bf B}(t)dt\nonumber\\
\end{eqnarray*}
\begin{eqnarray*}
\Longrightarrow\;\int{\bf A}(t)\;&\cdot&\;\frac{d{\bf B}(t)}{dt}\;=\;{\bf A}(t)\;\cdot\;{\bf B}(t)\;-\;\int\frac{d{\bf A}(t)}{dt}\;\cdot\;{\bf B}(t)dt\nonumber\\
\end{eqnarray*}
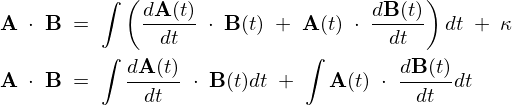
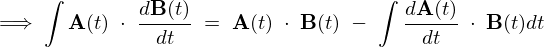
���ς̎��Ԕ���
\[
\frac{d}{dt}\left({\bf A}(t)\;\cdot\;{\bf A}(t)\right)\;=\;0
\]
\begin{eqnarray*}
\qquad\qquad\frac{d}{dt}\left({\bf A}(t)\;\cdot\;{\bf A}(t)\right)\;=\;\frac{d{\bf A}(t)}{dt}\cdot{\bf A}(t)\;+\;{\bf A}(t)\cdot\frac{d{\bf A}(t)}{dt}\nonumber\\
=\;2\;\frac{d{\bf A}(t)}{dt}\;\cdot\;{\bf A}(t)\nonumber\\
\end{eqnarray*}
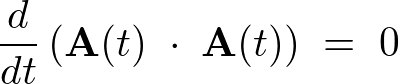
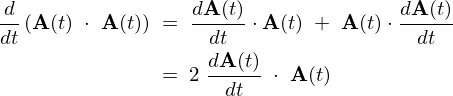
�x�N�g���ϕ��Ɋւ���d�v�Ȑ���
\[
\int{\bf A}(t)\;\cdot\;\frac{d{\bf A}(t)}{dt}\;dt\;=\;\frac{1}{2}\;{\bf A}(t)\;\cdot\;{\bf A}(t)
\]
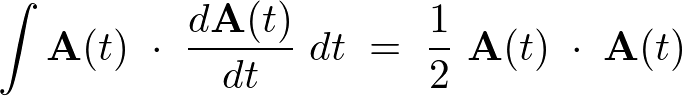
3�����x�N�g����̔��U�i�_�C�o�[�W�F���X�j
\begin{eqnarray*}
div{\bf A}(x,y,z)\;&=&\;\frac{\partial A_x(x,y,z)}{\partial x}\;+\;\frac{\partial A_y(x,y,z)}{\partial y}\;+\;\frac{\partial A_z(x,y,z)}{\partial z}\nonumber\\
&=&\;\underbrace{\left(\frac{\partial }{\partial x}\;,\quad\frac{\partial }{\partial y}\;,\quad\frac{\partial }{\partial z}\right)}\;\cdot\;\Big(A_x(x,y,z)\;,\quad A_y(x,y,z)\;,\quad A_z(x,y,z)\Big)\nonumber\\
&&\:\qquad\qquad\nabla\nonumber\\
&=&\;\nabla\;\cdot\;{\bf A}(x,y)\nonumber\\
\end{eqnarray*}
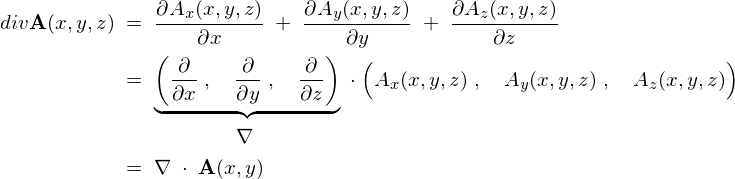
�x�N�g����̓R�[�h�֘A�y�[�W
- �m�����x���ƕϐ��ϊ�LaTeX�R�[�h�u����
- �m�����x���ƕϐ��ϊ��Ŏg��ꂽLaTeX�R�[�h�u����ɂȂ�܂��B���̂܂܃R�s�y����LaTeX��document�Ԃɓ\���ăR���p�C�������DVI�t�@�C���Ƃ��ďo�͂ł��܂��B�܂�TeXclip�l�̂Ƃ���ł����̂܂ܒ���t���������ping�摜�������ł��܂��B�������ߔN�����ȓ��p�T�C�g���ꕔ�ɂ����ĎU�������̂ŎQ�l�ɂ���ꍇ�͏Љ���N��\��Ȃǂ̑Ή��͕K�����肢�������܂��B
- ���ϗʊm���x�N�g���̌v�ZLaTeX�R�[�h�u����
- �������v�w�̃R���e���c�u���ϗʊm���x�N�g���̌v�Z�v�Ŏg��ꂽTeX�R�[�h�u����ɂȂ�܂��B���ۂɏo�͂��ăG���[�Ή��ς݂Ȃ̂ł��̂܂܃R�s�y����LaTeX�R���o�[�g��TeXClip�l�̂Ƃ���œ\��t���ăR���o�[�g��������Ɏg�p�ł��܂��B�������g�p����ꍇ�̓o�b�N�����N�Ȃǂ�K�����肢�������܂��B
- ���U�����U�s��LaTeX�R�[�h�u����
- �������v�w�̃R���e���c�u���U�����U�s��v�Ŏg��ꂽTeX�R�[�h�u����ɂȂ�܂��B���ۂɏo�͂��ăG���[�Ή��ς݂Ȃ̂ł��̂܂܃R�s�y����LaTeX�R���o�[�g��TeXClip�l�̂Ƃ���œ\��t���ăR���o�[�g��������Ɏg�p�ł��܂��B�������g�p����ꍇ�̓o�b�N�����N�Ȃǂ�K�����肢�������܂��B
- ���v���X�ϊ��R�[�h�u����
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B























