���v���X�ϊ��Ŏg����LaTeX�R�[�h�u����B
���̂܂܃R�s�y���č쐬�ł��܂��B
�Ȃ��ȉ��̃T�C�g�l�A
�ɂ����āA�R�[�h�����̂܂܃R�s�y����ΊȒP�ɐ����摜���쐬����܂��B
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:1\:\right]\;&=&\;\int^{\infty}_{0}1\cdot e^{-st}dt\nonumber\\
&=&\;\int^{\infty}_{0}\cdot e^{-st}dt\nonumber\\
&=&\;\left[\:-\frac{1}{s}e^{-st}\:\right]^{\infty}_{0}\nonumber\\
&=&\;-\frac{1}{s}\left(\:e^{-\infty}\;-\;e^{-0}\:\right)\nonumber\\
&=&\;\frac{1}{s}\nonumber\\
\end{eqnarray*}
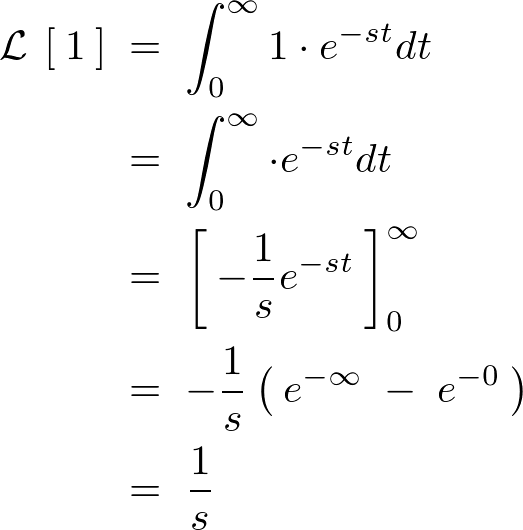
$f\left(\:t\:\right)\;=\;t$
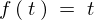
\[
F\left(\:s\:\right)\;=\;\mathcal{\:L\:}\left[\:f\left(\:t\:\right)\:\right]\;=\;\mathcal{\:L\:}\left[\:t\:\right]
\]
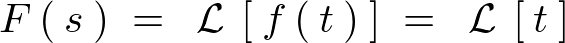
\begin{eqnarray*}
\mathcal{L}\left[\:t\:\right]\:=\:\frac{1}{s^2}
\end{eqnarray*}
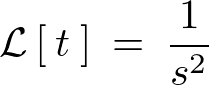
\begin{eqnarray*}
F\left(\:s\:\right)\:&=&\:\int^{\infty}_{0}t\cdot e^{-st}\:dt\nonumber\\
&=&\:\left[\:t\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}\:-\:\int^{\infty}_{0}\frac{dt}{dt}\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)dt\nonumber\\
&=&\:\qquad 0\qquad +\qquad\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\nonumber\\
\end{eqnarray*}
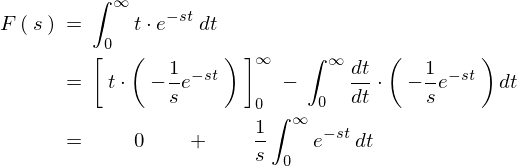
\begin{eqnarray*}
\Longrightarrow\qquad\mathcal{L}\left[\:t\:\right]\:=\:\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\nonumber\\
\end{eqnarray*}
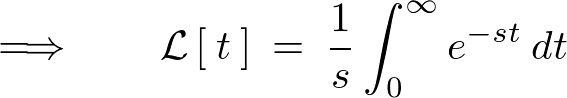
\begin{eqnarray*}
\mathcal{L}\left[\:t\:\right]\:&=&\:\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\nonumber\\
&=&\:\frac{1}{s}\left[\:-\frac{1}{s}e^{-st}\:\right]^{\infty}_{0}\nonumber\\
&=&\:-\frac{1}{s^2}\left(\:e^{-\infty}\;-\;e^{0}\:\right)\nonumber\\
&=&\:\frac{1}{s^2}\nonumber\\
\end{eqnarray*}
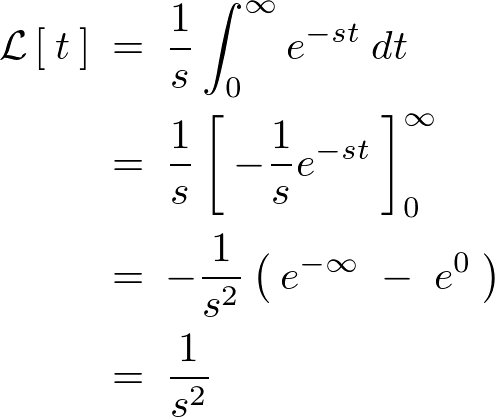
\begin{eqnarray*}
\mathcal{L}\left[\:t\:\right]\:=\:\frac{1}{s^2}
\end{eqnarray*}
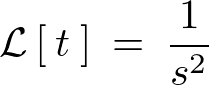
$f\left(\:t\:\right)\;=\;t^2$
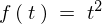
\[
F\left(\:s\:\right)\;=\;\mathcal{L}\left[\:f\left(\:t\:\right)\:\right]\;=\;\mathcal{\:L\:}\left[\:t^2\:\right]
\]
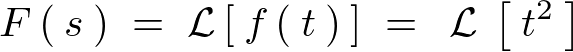
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:t^2\:\right]\;&=&\;\int^{\infty}_{0}t^2\cdot e^{-st}dt\nonumber\\
&=&\;\left[\:t^2\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}-\int^{\infty}_{0}\frac{d\:t^2}{dt}\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)dt\nonumber\\
&=&\;0\;+\;\frac{1}{\;s\;}\int^{\infty}_{0}2t\cdot e^{-st}dt\nonumber\\
&=&\;\frac{2}{\;s\;}\int^{\infty}_{0}t\cdot e^{-st}dt\nonumber\\
&=&\;\frac{2}{\;s\;}\left\{\;\left[\:t\cdot\left(\:-\frac{1}{\;s\;}e^{-st}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d}{dt}t\cdot\left(\:-\frac{1}{\;s\;}e^{-st}\:\right)dt\;\right\}\nonumber\\
&=&\;\frac{2}{\;s\;}\left(\:\quad 0\quad \;+\;\frac{1}{\;s\;}\int^{\infty}_{0}e^{-st}dt\:\right)\nonumber\\
&=&\;\frac{2}{\;s^2\:}\int^{\infty}_{0}e^{-st}dt\nonumber\\
&=&\;\frac{2}{\;s^2\:}\left[\:-\frac{1}{\;s\;}e^{-st}\:\right]^{\infty}_{0}\nonumber\\
&=&\;-\frac{2}{\:s^3\:}\Big[\:e^{-\infty}\;-\;e^0\:\Big]\nonumber\\
&=&\;\frac{2}{\:s^3\:}\nonumber\\
\end{eqnarray*}
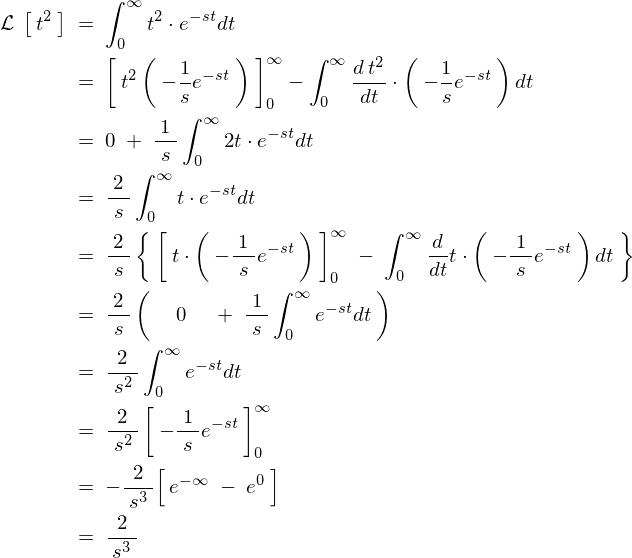
\begin{eqnarray*}
\mathcal{\:F\:}\left(\:s\:\right)\;=\;\mathcal{\:L\:}\left[\:f\left(\:t\:\right)\:\right]\;=\;\mathcal{\:L\:}\left[\:t^2\:\right]\;=\;\frac{2}{s^3}
\end{eqnarray*}
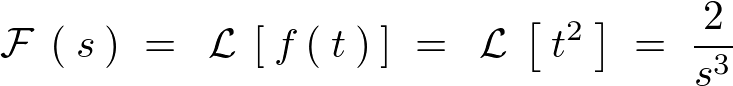
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:t^2\:\right]\;=\;\frac{2}{s^3}
\end{eqnarray*}
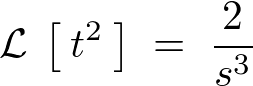
\begin{eqnarray*}
F\left(\:s\:\right)\;&=&\;\int^{\infty}_{0}t^3\cdote^{-st}dt\;\nonumber\\
&=&\;\left[\:t^3\cdot\left(\:-\frac{1}{\;s\;}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d}{dt}t^3\cdot\left(\:-\frac{1}{\;s\;}e^{-st}\:\right)dt\nonumber\\
&=&\qquad 0\qquad +\;\frac{1}{s}\int^{\infty}_{0}3t^2\cdot e^{-st}dt\nonumber\\
&=&\;\frac{3}{s}\left[\:\int^{\infty}_{0}t^2\cdot e^{-st}\:\right]\nonumber\\
&=&\;\frac{3}{s}\cdot\frac{2}{s^3}\nonumber\\
&=&\;\frac{3\cdot 2}{s^4}\nonumber\\
\end{eqnarray*}
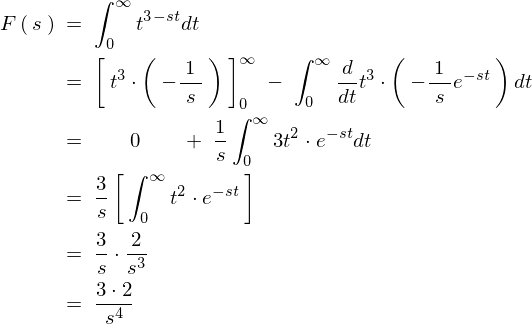
\begin{eqnarray*}
F\left(\:s\:\right)\;&=&\;\int^{\infty}_{0}t^4\cdot e^{-st}dt\nonumber\\
&=&\;\left[\:t^4\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d\;t^4}{dt}\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)dt\nonumber\\
&=&\qquad 0 \qquad +\;\frac{1}{s}\int^{\infty}_{0}4t^3\cdot e^{-st}dt\nonumber\\
&=&\;\frac{4}{s}\left[\:\int^{\infty}_{0}t^3\cdot e^{-st}dt\:\right]\nonumber\\
&=&\;\frac{4}{s}\cdot\left(\:\frac{3\cdot 2}{s^4}\:\right)\nonumber\\
&=&\;\frac{4\cdot 3\cdot 2\cdot}{s^5}\nonumber\\
&=&\;\frac{4!}{s^5}\nonumber\\
\end{eqnarray*}
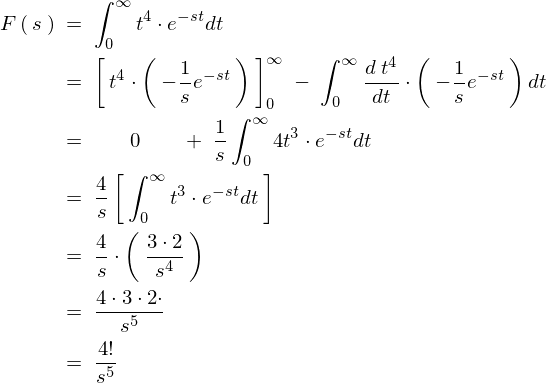
\[
\Longrightarrow\qquad \mathcal{\:L\:}\left[t^n\right]\;=\;\frac{n!}{s^{n\;+\;1}}
\]
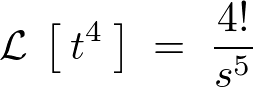
�O�p���̃��v���X�ϊ�
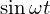 �̃��v���X�ϊ�
�̃��v���X�ϊ�
\[
\mathcal{\:L\:}\left[\:\sin\omega t\:\right]\;=\;\int^{\infty}_{0}e^{-st}\cdot\sin\omega\:t\:dt
\]
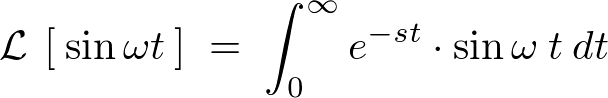
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:\sin\omega t\:\right]\;&=&\;\int^{\infty}_{0}e^{-st}\cdot\sin\omega\:t\:dt\nonumber\\
\int^{\infty}_{0}e^{-st}\cdot\sin\omega\:t\:dt\;&=&\;\left[\:\sin\omega\:t\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d\:\sin\omega\:t}{dt}\left(\:-\frac{1}{s}e^{-st}\:\right)\nonumber\\
&=&\;\left[\:\sin\omega\:t\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d\:\sin\omega\:t}{dt}\left(\:-\frac{1}{s}e^{-st}\:\right)\nonumber\\
&=&\;\qquad 0 \qquad \;+\;\frac{1}{s}\int^{\infty}_{0}e^{-st}\cdot\omega\cos\omega\:t\:dt\nonumber\\
&=&\;\frac{\omega}{s}\int^{\infty}_{0}e^{-st}\cdot \cos\omega\:dt\nonumber\\
\end{eqnarray*}
\[
\int^{\infty}_{0}e^{-st}\cdot\sin\omega\:t\:dt\;=\;\frac{\omega}{s}\int^{\infty}_{0}e^{-st}\cdot \cos\omega\:dt\nonumber\\
\]
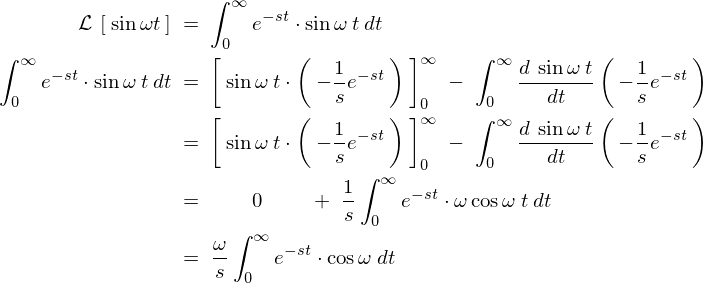
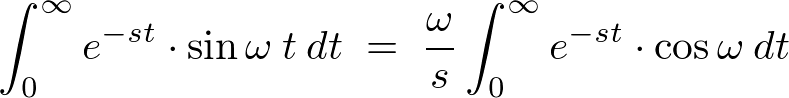
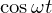 �̃��v���X�ϊ�
�̃��v���X�ϊ�
\[
\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\;=\;\int^{\infty}_{0}e^{-st}\cdot \cos \omega tdt
\]
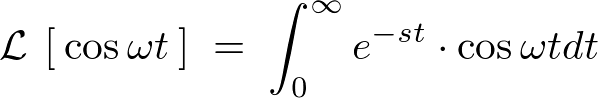
\begin{eqnarray*}
\int^{\infty}_{0}e^{-st}\cdot \cos \omega tdt\;&=&\;\left[\;\cos\omega t\left(\:-\frac{1}{s}e^{-st}\:\right)\;\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d\:\cos\omega t}{dt}\left(\:-\frac{1}{s}e^{-st}\:\right)dt\nonumber\\
&=&\;\frac{1}{s}\;+\;\frac{1}{s}\int^{\infty}_{0}\left(\:-\omega\cdot\sin\omega t\:\right)\cdot e^{-st}dt\nonumber\\
&=&\;\frac{1}{s}\;-\;\frac{\omega}{s}\int^{\infty}_{0}e^{-st}\cdot\sin\omega tdt\nonumber\\
\end{eqnarray*}
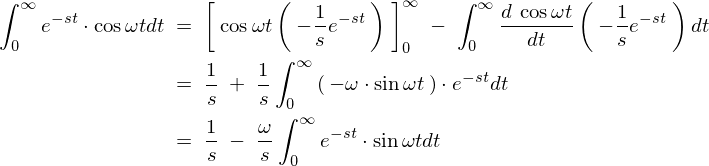
\begin{eqnarray*}
I\;&\equiv&\;\int^{\infty}_{0}e^{-st}\cdot\sin\omega tdt\nonumber\\
&=&\;\left[\:\sin\omega t\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d\:\sin\omega t}{dt}\left(\:-\frac{1}{s}e^{-st}\:\right)dt\nonumber\\
&=&\;\qquad 0 \qquad\;+\;\qquad\frac{1}{s}\int^{\infty}_{0}\omega\cdot\cos\omega t\cdot e^{-st}dt\nonumber\\
&=&\;\frac{\omega}{s}\int^{\infty}_{0}\cos\omega t\cdot e^{-st}dt\nonumber\\
\end{eqnarray*}
\[
\int^{\infty}_{0}e^{-st}\cdot\sin\omega tdt\;=\;\frac{\omega}{s}\int^{\infty}_{0}\cos\omega t\cdot e^{-st}dt\nonumber\\
\]
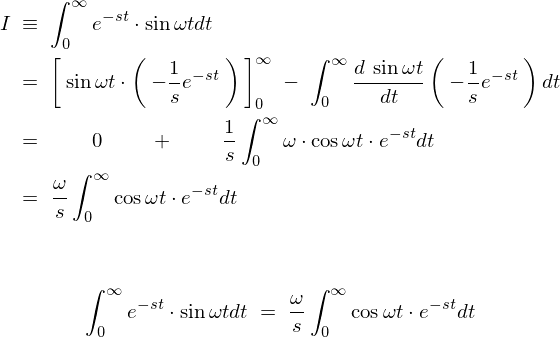
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\;=\;\frac{1}{s}\;-\;\frac{\omega}{s}\left(\:\int^{\infty}_{0}e^{-st}\cdot\sin\omega tdt\:\right)\nonumber\\
=\;\frac{1}{s}\;-\;\frac{\omega}{s}\left(\:\frac{\omega}{s}\int^{\infty}_{0}\cos\omega t\cdot e^{-st}dt\:\right)\nonumber\\
=\;\frac{1}{s}\;-\;\frac{\omega}{s}\left(\:\frac{\omega}{s}\cdot\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\:\right)\nonumber\\
=\;\frac{1}{s}\;-\;\frac{\omega^2}{s^2}\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\nonumber\\
\end{eqnarray*}
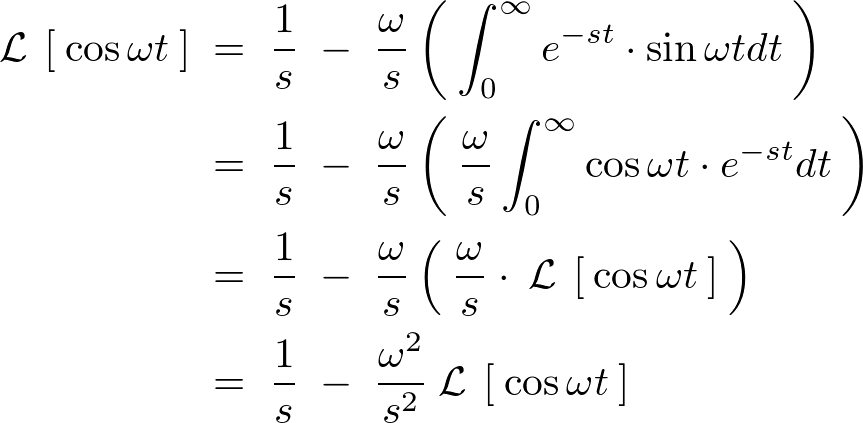
\begin{eqnarray*}
\left(\:1 \;+\;\frac{\omega^2}{s^2}\:\right)\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\;&=&\;\frac{1}{s}\nonumber\\
\frac{s^2\;+\;\omega^2}{s^2}\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\;&=&\;\frac{1}{s}\nonumber\\
\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\;&=&\;\frac{s^2}{s^2\;+\;\omega^2}\frac{1}{s}\nonumber\\
\end{eqnarray*}
\[
\mathcal{\:L\:}\left[\:\cos\omega t\:\right]\;=\;\frac{s}{s^2\;+\;\omega^2}\nonumber\\
\]
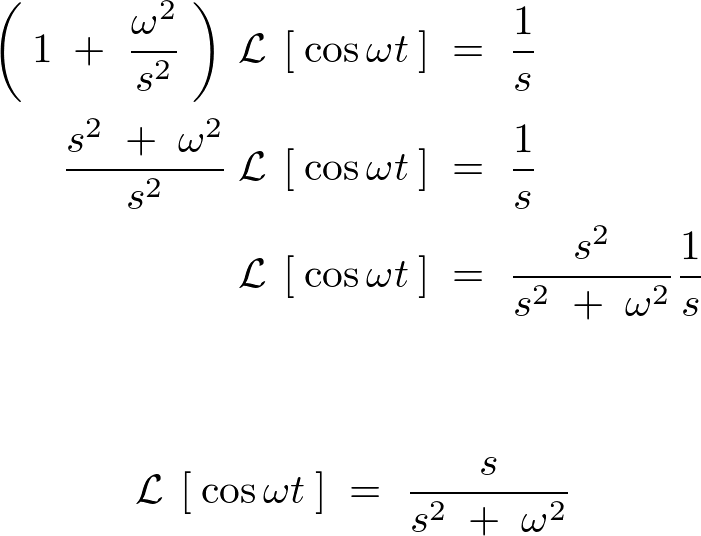
���v���X�ϊ��R�[�h�u����֘A�y�[�W
- �m�����x���ƕϐ��ϊ�LaTeX�R�[�h�u����
- �m�����x���ƕϐ��ϊ��Ŏg��ꂽLaTeX�R�[�h�u����ɂȂ�܂��B���̂܂܃R�s�y����LaTeX��document�Ԃɓ\���ăR���p�C�������DVI�t�@�C���Ƃ��ďo�͂ł��܂��B�܂�TeXclip�l�̂Ƃ���ł����̂܂ܒ���t���������ping�摜�������ł��܂��B�������ߔN�����ȓ��p�T�C�g���ꕔ�ɂ����ĎU�������̂ŎQ�l�ɂ���ꍇ�͏Љ���N��\��Ȃǂ̑Ή��͕K�����肢�������܂��B
- ���ϗʊm���x�N�g���̌v�ZLaTeX�R�[�h�u����
- �������v�w�̃R���e���c�u���ϗʊm���x�N�g���̌v�Z�v�Ŏg��ꂽTeX�R�[�h�u����ɂȂ�܂��B���ۂɏo�͂��ăG���[�Ή��ς݂Ȃ̂ł��̂܂܃R�s�y����LaTeX�R���o�[�g��TeXClip�l�̂Ƃ���œ\��t���ăR���o�[�g��������Ɏg�p�ł��܂��B�������g�p����ꍇ�̓o�b�N�����N�Ȃǂ�K�����肢�������܂��B
- ���U�����U�s��LaTeX�R�[�h�u����
- �������v�w�̃R���e���c�u���U�����U�s��v�Ŏg��ꂽTeX�R�[�h�u����ɂȂ�܂��B���ۂɏo�͂��ăG���[�Ή��ς݂Ȃ̂ł��̂܂܃R�s�y����LaTeX�R���o�[�g��TeXClip�l�̂Ƃ���œ\��t���ăR���o�[�g��������Ɏg�p�ł��܂��B�������g�p����ꍇ�̓o�b�N�����N�Ȃǂ�K�����肢�������܂��B
- �x�N�g����̓R�[�h
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B























