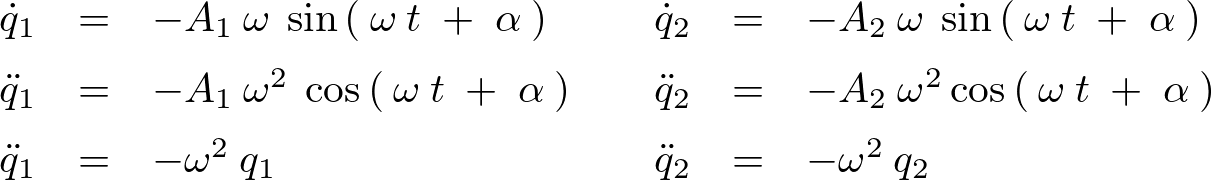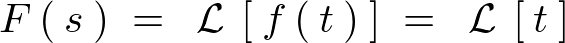解析力学コンテンツ連成振動の解-3重バネの振動LaTeXコード
現在新規ドメインコンテンツ「微分方程式いろいろ」を作成しいている最中でそれ用に使用された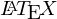
のコード一覧です。
多忙のため説明書きはなしでコードとその出力画像のみの投稿になります。
コードの記述方法に関して知りたい場合は書籍や検索などするか、あるいは実際のローカル環境に落としたTeXシステム上でのDVIファイル出力、またはTeXclip様のところで直接出力して自分でいろいろ試してみればわかると思うのでそちらの方向でお願いしまｽﾐﾀﾞ<｀ω´>。
３重バネのラグランジアン
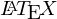コード
\begin{eqnarray*}
L\;=\;\frac{1}{2}\:m\:\left(\:\dot{q}^{2}_{1}\;+\;\dot{q}^{2}_{2}\:\right)\;-\;\frac{1}{2}\:c\:q^{2}_{1}\;-\;\frac{1}{2}\:k\:\left(\:q_{2}\:-\:q_{1}\:\right)^{2}\;-\;\frac{1}{2}\:c\:q^{2}_{2}
\end{eqnarray*}
出力画像
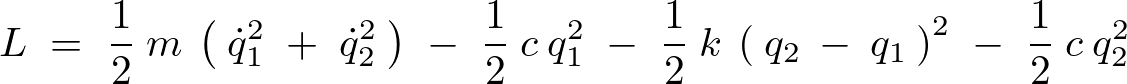
コード
\begin{eqnarray}
&\begin{array}{rcc}\vspace{5pt}
\frac{d}{dt}\left(\:m\:\dot{q}_{1}\:\right)\:&=&\:-c\:q_{1}\;+\;k\:\left(\:q_{2}\:-\:q_{1}\:\right)\\
m\:\ddot{q}_{1}\:&=&\:-c\:q_{1}\;+\;k\:\left(\:q_{2}\:-\:q_{1}\:\right)
\end{array}&\hspace{-80pt}\\
&\hspace{-3pt}\begin{array}{rcc}\vspace{5pt}
\frac{d}{dt}\:\left(\:m\dot{q}_{2}\:\right)\:&=&\:-c\:q_{2}\:-\:k\left(\:q_{2}\:-\:q_{1}\:\right)\\
m\:\ddot{q}_{2}\:&=&\:-c\:q_{2}\:-\:k\left(\:q_{2}\:-\:q_{1}\:\right)
\end{array}&\hspace{-80pt}
\end{eqnarray}
出力画像
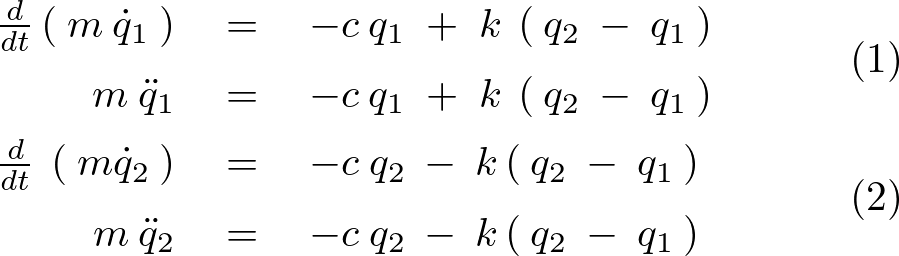
コード
\begin{eqnarray*}
\left\{\begin{array}{ccc}\vspace{5pt}
q_1\:&\equiv&\:A_1\:\cos\left(\:\omega\:t\;+\;\alpha\:\right)\\
q_2\:&\equiv&\:A_2\:\cos\left(\:\omega\:t\;+\;\alpha\:\right)
\end{array}\right.
\end{eqnarray*}
出力画像
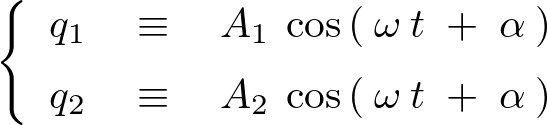
コード
\[
\begin{array}{cclcccl}\vspace{5pt}
\dot{q}_{1}&=&-A_{1}\:\omega\:\sin\left(\:\omega\:t\;+\;\alpha\:\right)&&\dot{q}_{2}&=&-A_{2}\:\omega\:\sin\left(\:\omega\:t\;+\;\alpha\:\right)\\\vspace{5pt}
\ddot{q}_{1}&=&-A_{1}\:\omega^{2}\:\cos\left(\:\omega\:t\;+\;\alpha\:\right)&&\ddot{q}_{2}&=&-A_{2}\:\omega^{2}\cos\left(\:\omega\:t\;+\;\alpha\:\right)\\\ddot{q}_{1}&=&-\omega^{2}\:q_{1}&&\ddot{q}_{2}&=&-\omega^{2}\:q_{2}
\end{array}
\]
出力画像
