���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
�R��������
�T�e���C�g�T�C�g�g�������������낢���h�̃R���e���c�Ńt���[�h�}�������[�g���F�����f���iE=V�̏ꍇ�ɂ�����3���������j�̃y�[�W�Ƀ~�X���������̂ł���̏C���������݉����Ă���Ƃ������Ƃ�����A�Ȃ̂ō����3�����������e�[�}�ɂ��Ă݂悤�Ǝv���܂��B
������3���������͏K��Ȃ��̂ň�ʓI�ɂ������������Ȃ��́H�Ǝv����l�����邩�Ǝv���܂�������Ȃ��Ƃ͂���܂���B
���Z�܂ł̕�������2���������܂łȂ炾��ł���������Ƃ����邩�Ǝv���܂��B
������3���������͏K��Ȃ��̂ň�ʓI�ɂ������������Ȃ��́H�Ǝv����l�����邩�Ǝv���܂�������Ȃ��Ƃ͂���܂���B

�܂����̂悤��3�����������l���A���ӂ�
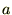 �Ŋ���܂��B
�Ŋ���܂��B
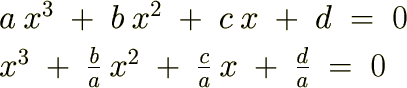
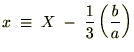
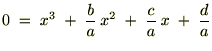
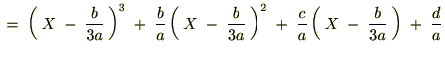
�@
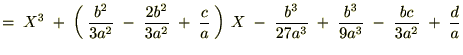
���̂悤�ȕϐ��ϊ������邱�Ƃɂ��Q���̍����Ȃ��Ȃ�܂��B �����Ō��₷���̂��߂Ɏ��̂悤�ɒu�����܂��B
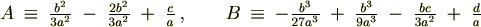
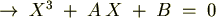
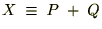 �ƕϐ��ϊ���������Čv�Z�𑱂��܂��B
�ƕϐ��ϊ���������Čv�Z�𑱂��܂��B
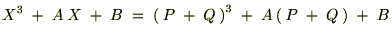
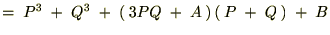
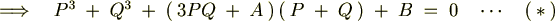
 �̎����������邽�߂ɂ͎��������ɂȂ�܂��B
�̎����������邽�߂ɂ͎��������ɂȂ�܂��B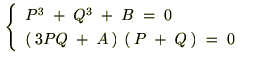
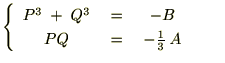
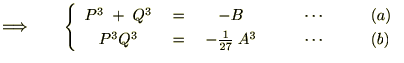
 ���A
���A
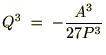
 �ɑ�����Č��������2�������������܂��B
�ɑ�����Č��������2�������������܂��B
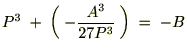
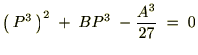
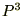 ��2�����������ƍl���邱�Ƃ��ł��܂��B
��2�����������ƍl���邱�Ƃ��ł��܂��B����ɂ�����2���������̉��̌������v���o���Ă���Ă͂߂��
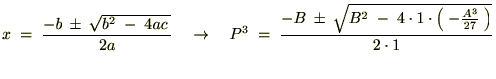
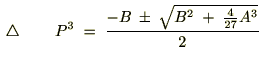
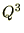 �ɑ��Ă��������Ƃ�������̂Ō��ǎ��̂悤�Ȏ������܂�܂��B
�ɑ��Ă��������Ƃ�������̂Ō��ǎ��̂悤�Ȏ������܂�܂��B
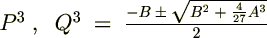
�����ł���3��̎��������͂܂�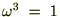 �Ȃ̂łP�B
�Ȃ̂łP�B
���̂��Ƃɂ��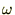 �́A
�����
�́A
�����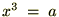 �̉���1�̗�����
�ƕ\���邱�Ƃ��l�������P��Q�̗��������Ƃ�ۂɂ������悤�ɂR�̏ꍇ���l����Ƃ܂��A
�̉���1�̗�����
�ƕ\���邱�Ƃ��l�������P��Q�̗��������Ƃ�ۂɂ������悤�ɂR�̏ꍇ���l����Ƃ܂��A
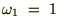 �̂Ƃ��A
�̂Ƃ��A
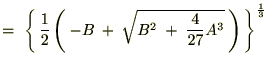
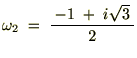 �̂Ƃ��A
�̂Ƃ��A
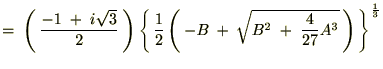
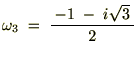 �̂Ƃ�
�̂Ƃ�
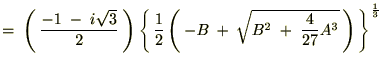
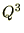 �������悤�ɂ��Ď��̂悤�ɂȂ�܂��B
�������悤�ɂ��Ď��̂悤�ɂȂ�܂��B
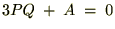 �ł��邽�߂ɂ�
�ł��邽�߂ɂ�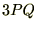 �������łȂ���Ȃ�Ȃ��̂ŁA���̂悤�ȑg�ݍ���ɂȂ�܂��B
����ɂ��A
�������łȂ���Ȃ�Ȃ��̂ŁA���̂悤�ȑg�ݍ���ɂȂ�܂��B
����ɂ��A
 �ł���̂ő������A
�ł���̂ő������A
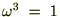 �Ȃ̂łP�B
�Ȃ̂łP�B���̂��Ƃɂ��
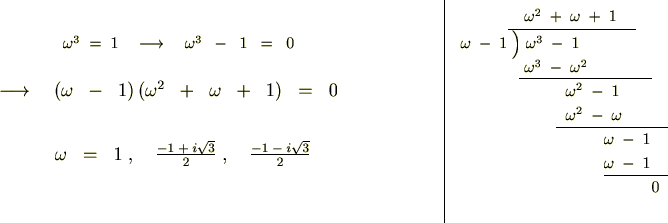
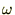 �́A
�́A
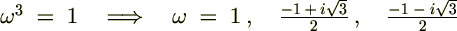
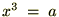 �̉���1�̗�����
�̉���1�̗�����
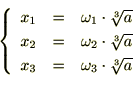
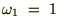 �̂Ƃ��A
�̂Ƃ��A
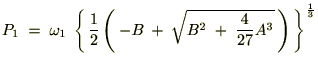
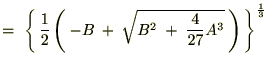
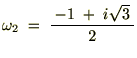 �̂Ƃ��A
�̂Ƃ��A
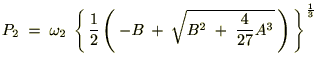
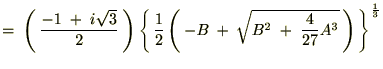
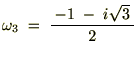 �̂Ƃ�
�̂Ƃ�
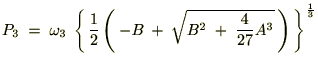
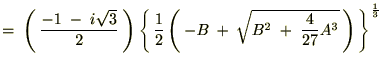
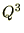 �������悤�ɂ��Ď��̂悤�ɂȂ�܂��B
�������悤�ɂ��Ď��̂悤�ɂȂ�܂��B
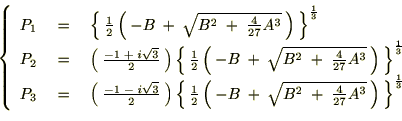
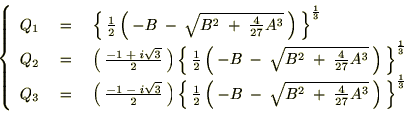
���̑g�ݍ��킹
���x�͉��̑g�ݍ��킹�ɂ��čl���܂��B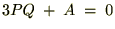 �ł��邽�߂ɂ�
�ł��邽�߂ɂ�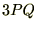 �������łȂ���Ȃ�Ȃ��̂ŁA���̂悤�ȑg�ݍ���ɂȂ�܂��B
�������łȂ���Ȃ�Ȃ��̂ŁA���̂悤�ȑg�ݍ���ɂȂ�܂��B
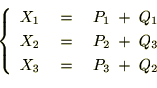
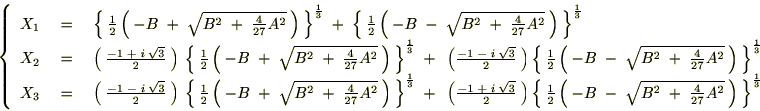
 �ł���̂ő������A
�ł���̂ő������A

�@


















