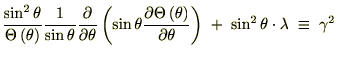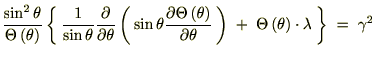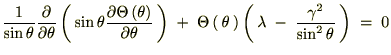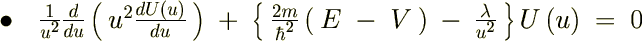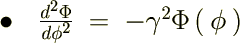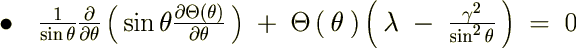���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
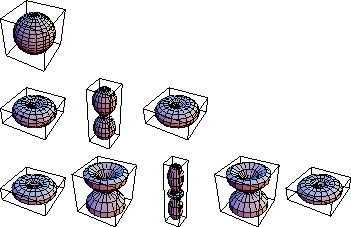
���̂悤�Ȏ����������Ƃ��܂��B
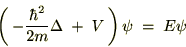
���ӂɂR���������ɂ�����Q�K�����̍�p�f�A�܂胉�v���V�A���������Ă��܂��B ������ɍ��W�ŕ\������Ƃǂ̂悤�Ȍ`�ɕό`�ł��邩���l���Ă݂܂��傤�B
�܂����v���V�A���̋ɍ��W�\���͎��̂悤�ɋ��܂�܂����B
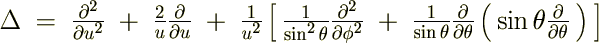
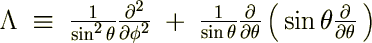
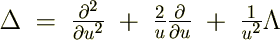
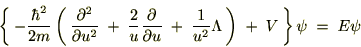
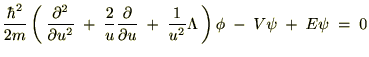
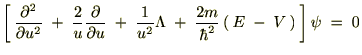
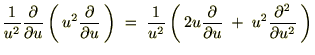
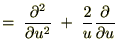
�̊W������̂Ŏ��̂悤�ɕ\���܂��B
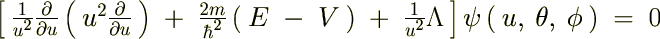
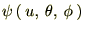 �Ɋւ��Ă̒��̕ϐ������̂悤�ɕ������čl���邱�Ƃɂ��܂��B
�Ɋւ��Ă̒��̕ϐ������̂悤�ɕ������čl���邱�Ƃɂ��܂��B
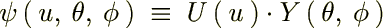
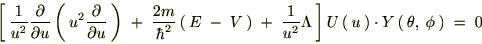
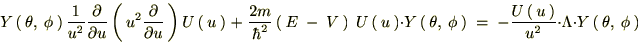
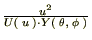 ���|���܂��B
���|���܂��B
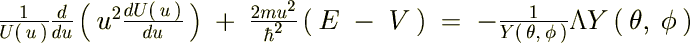
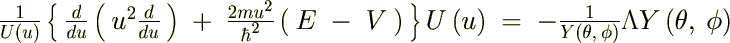
���̏o�Ă�����������킩��悤�ɗ��ӂ����ꂼ��̕ϐ��ɕ�����Ă���A
���̂悤�Ȍ`�ɂł����Ƃ��݂��̕ϐ���萔�Ƃ݂Ȃ����Ƃ��ł��܂��B��������������ϐ������`�ƌ������肵�܂��B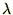 �ƒu���Ă��ꂼ���ό`���Ă����܂��B
�ƒu���Ă��ꂼ���ό`���Ă����܂��B
���̂悤�Ȍ`�ɂł����Ƃ��݂��̕ϐ���萔�Ƃ݂Ȃ����Ƃ��ł��܂��B��������������ϐ������`�ƌ������肵�܂��B
���̒萔��
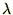 �ƒu���Ă��ꂼ���ό`���Ă����܂��B
�ƒu���Ă��ꂼ���ό`���Ă����܂��B 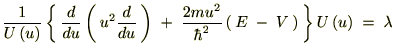
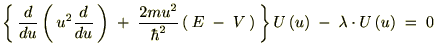
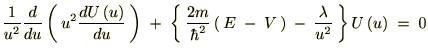
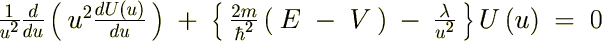
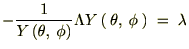
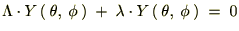
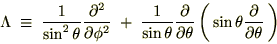
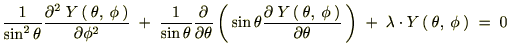
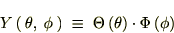
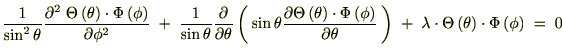
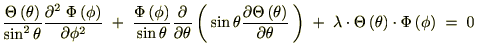
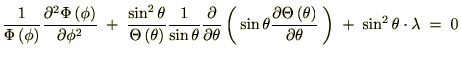
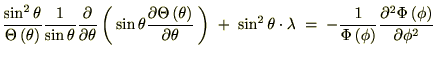
���x�͂��ꂼ��̒萔��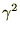 �ƒu���܂��B
�ƒu���܂��B
�܂��A
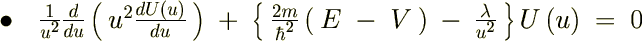
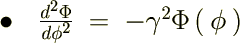
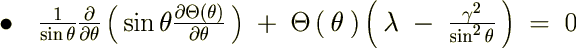
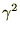 �ƒu���܂��B
�ƒu���܂��B�܂��A