���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
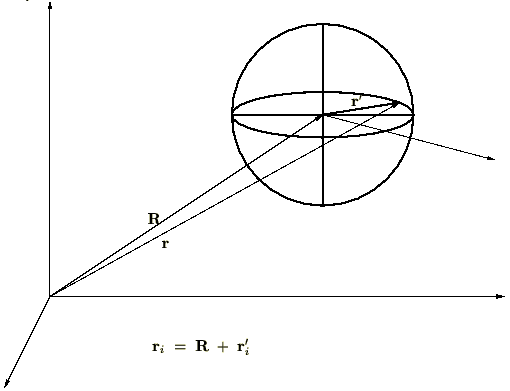
�ɍ��W�ɂ����鎞�Ԕ����͎��̂悤�Ȃ��̂ł����B

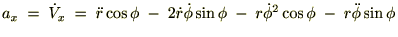
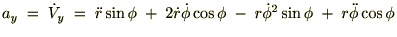
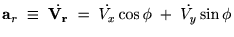
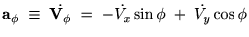
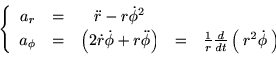
�ɍ��W�Ǝ��Ԕ���
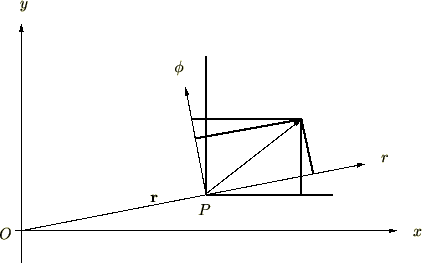
���}�ɂ�����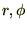 �͌Œ肳��܂���B���̊p�x�͎���
�͌Œ肳��܂���B���̊p�x�͎���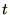 �ɂ���ĕω����܂��B
�ɂ���ĕω����܂��B
�p�x�̎��Ԕ���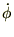 ���p���x�ƌĂсA�^�����~�^���ł���ꍇ�A
���p���x�ƌĂсA�^�����~�^���ł���ꍇ�A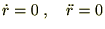 �ł���̂�
�ł���̂�
���ӂ���_���y���܂Ƃ߂�ƍ��W�\���Œ��ӂ���_�ɑ���
�Ƃ������Ƃ������邩�Ǝv���܂��B
�]���ċɍ��W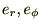 �ɂ����đ��x�����ڕ\������Ƃ��͍��W���̎��Ԉˑ����l�����Ȃ���Ȃ�܂���B
�ɂ����đ��x�����ڕ\������Ƃ��͍��W���̎��Ԉˑ����l�����Ȃ���Ȃ�܂���B
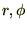 �͌Œ肳��܂���B���̊p�x�͎���
�͌Œ肳��܂���B���̊p�x�͎���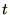 �ɂ���ĕω����܂��B
�ɂ���ĕω����܂��B
�p�x�̎��Ԕ���
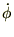 ���p���x�ƌĂсA�^�����~�^���ł���ꍇ�A
���p���x�ƌĂсA�^�����~�^���ł���ꍇ�A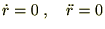 �ł���̂�
�ł���̂�
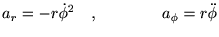
���ӂ���_���y���܂Ƃ߂�ƍ��W�\���Œ��ӂ���_�ɑ���
|
�ɍ��W�@���@ |
�]���ċɍ��W
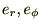 �ɂ����đ��x�����ڕ\������Ƃ��͍��W���̎��Ԉˑ����l�����Ȃ���Ȃ�܂���B
�ɂ����đ��x�����ڕ\������Ƃ��͍��W���̎��Ԉˑ����l�����Ȃ���Ȃ�܂���B
|
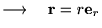 |
|---|---|
���Ԕ����i���x�j |
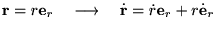 |
�ɍ��W�̎��ԕω� |
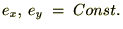 |
����ɋɍ��W�ɂ������{�x�N�^�[�̑��x�����߂�ƁA
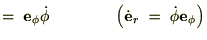
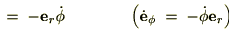
�]���ċɍ��W�\���̑��x�͎��̂悤�ɂȂ�܂��B
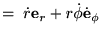
�Â��ĉ����x�����߂�A
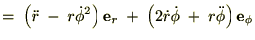
�ƂȂ�̂���ق��Ɠ��l�̌��ʂ������܂��B

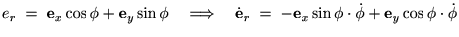
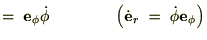
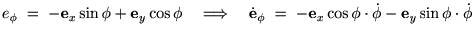
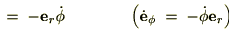
�]���ċɍ��W�\���̑��x�͎��̂悤�ɂȂ�܂��B
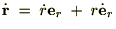
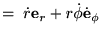
�Â��ĉ����x�����߂�A
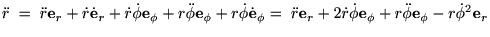
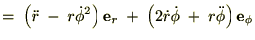


�ɍ��W�̎��Ԕ����֘A�y�[�W
- ���W�ϊ��Q
- �f�J���g���W�ɂ������p�f�i�I�y���[�^�[�j���ɍ��W�ɕϊ�����ߒ����l�@���܂��B
- ���W�ϊ��P
- �f�J���g���W�ɂ������p�f�i�I�y���[�^�[�j���ɍ��W�ɕϊ�����ߒ����l�@���܂��B
- �ɍ��W�ւ̕ϊ�
- �f�J���g���W����ɍ��W�ցB���̃y�[�W�ł͋ɍ��W�ɂ��^���̋L�q�ɂ��čl�@���܂��B
- �ɍ��W���v���V�A��
- �f�J���g���W�ɂ�����2�����I�y���[�^�[���ɍ��W�ɕϊ������̂����x��3�����Ɋg�����Ă��̃I�y���[�^�[���ɍ��W�n�ɂ����Ăǂ̂悤�ɕ\���ł���̂����l�@���܂��B
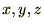 ���W�@���@�Œ�
���W�@���@�Œ�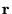 �ƈꏏ�Ɏ����ړ�����
�ƈꏏ�Ɏ����ړ�����
















