���m�点
��Web�T�C�g�̓T�C�g�쐬�V�X�e���̐[���Ȍ��ׂɂ�茻�݃����N�̕ύX���s���Ă���܂��B�Ǘ��l�����Z�̂��߃��_�C���N�g�T�C�g�͍쐬�����A���ڃ����N�ύX���s���\��ł��B�������������������B�����͖���ɂȂ�܂��B
�����̃y�[�W�͂Ȃ�ׂ��c���悤�ɂ��܂������ŕύX���܂��̂Ńu�b�N�}�[�N�Ȃǂ��Ă�����́A���ʓ|�ɂȂ邩�Ǝv���܂������̃h���C��https://mathematical.jp/mathematical/�@����ړI�̃y�[�W�ɍs���悤�ɂ��肢�\���グ�܂��B
���ʋɍ��W�ɂ�����I�y���[�^�[�ϊ�
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/tex_mathematica2013img1.png)
�f�J���g���W�n�ɂ�����
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img5.png) ���A
���A
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img3.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img4.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img5.png) �Ɋւ��Ď����̕ϐ�
�Ɋւ��Ď����̕ϐ�![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/r_phi_small_img.png) �ł̈ꎟ�ߎ��ł̊��̕ω��ʂ͑S�����ɂ���Ď��̂悤�ɗ^�����܂��B
�ł̈ꎟ�ߎ��ł̊��̕ω��ʂ͑S�����ɂ���Ď��̂悤�ɗ^�����܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img7.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img1.png)
�܂�
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_small_img1.png) �̂ق�����v�Z���Ă����܂��B
�̂ق�����v�Z���Ă����܂��B��L�̎��ɑ��Ă����
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_small_img1.png) �ɂ��Δ������{���܂��B
�ɂ��Δ������{���܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img8.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img9.png) �y�ё�3����
�y�ё�3����![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img10.png) �̕�����
�̕�����![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/r_small_img.png) ��
��![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/phi_small_img.png) �Ń`�F�[�������܂��B
�Ń`�F�[�������܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img13.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img14.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img15.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img16.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img17_1.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img18_1.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img19.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img20.png)
����Ď��̂悤�Ȍ��ʂɂȂ�܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img21.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/y_small_img1.png) �̃I�y���[�^�[�Ɋւ��đS�����́A
�̃I�y���[�^�[�Ɋւ��đS�����́A
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img23.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img24.png)
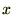 �̎��Ɠ����悤�ɏ�L���̑�1���Ƒ�3�����`�F�[�������܂��B
�̎��Ɠ����悤�ɏ�L���̑�1���Ƒ�3�����`�F�[�������܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img26_1.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img27.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img28.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img29.png)
�Δ����������̋�̓I�Ȍv�Z
���Ɋe�X�̕Δ������̌v�Z�����ꂼ��s���Ă݂܂��傤�B![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/r_phi_small_img.png) ��
��![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_y_small_img.png) �̊Ԃɂ͂��ꂼ�ꎟ�̂悤�ȊW����������܂��B
�̊Ԃɂ͂��ꂼ�ꎟ�̂悤�ȊW����������܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img30.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_y_small_img.png) �̂��ꂼ��ɂ����ĕΔ������{���Ă����܂��B
�̂��ꂼ��ɂ����ĕΔ������{���Ă����܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img31.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img32.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/r_small_img.png) ��
��![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_small_img1.png) �ɂ��Δ������ʂ͎��̂悤�ɂȂ�܂��B
�ɂ��Δ������ʂ͎��̂悤�ɂȂ�܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img33.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img34.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img35.png) �̔����Ɋւ��Ă͂܂�
�̔����Ɋւ��Ă͂܂�![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/y_over_x_small_img.png) ��
��![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/t_small_img.png) �ƒu���Ēu���������
�ƒu���Ēu���������![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_small_img1.png) �Ŕ������܂��B
�Ŕ������܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img38.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img39.png) �ƂȂ肱���
�ƂȂ肱���![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/phi_small_img.png) �Ŕ�������Ǝ��̂悤�ɂȂ�܂��B
�Ŕ�������Ǝ��̂悤�ɂȂ�܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img40.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img41.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img41.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img42.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img43.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img44.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/phi_small_img.png) ��
��![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/x_small_img1.png) �Ŕ������邽�߂�
�Ŕ������邽�߂�![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/t_small_img.png) �Ń`�F�[�������܂��B
�Ń`�F�[�������܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img45.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img46.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img47.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img48.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img49.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img50.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img51.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img52.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img53.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img54.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img55.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img56.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img57.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/phi_small_img.png) �ɂ��Ă����l�ɕΔ������{���܂��B
�ɂ��Ă����l�ɕΔ������{���܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img58.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img59.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img60.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img61.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img62.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img63.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img64.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/y_small_img1.png) �ɂ��Ă����l�̕Δ������{���Ύ��̂悤�ɋ��܂�܂��B
�ɂ��Ă����l�̕Δ������{���Ύ��̂悤�ɋ��܂�܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img65.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img66.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img67.png) �̕ϊ����ɂ��ꂼ�������Ă����܂��B
�̕ϊ����ɂ��ꂼ�������Ă����܂��B
���W�ϊ��P�֘A�y�[�W
- ���W�ϊ��Q
- �f�J���g���W�ɂ������p�f�i�I�y���[�^�[�j���ɍ��W�ɕϊ�����ߒ����l�@���܂��B
- �ɍ��W�̎��Ԕ���
- ��]���W�n�ɂ����鎞�Ԕ������l�@���܂��B
- �ɍ��W�ւ̕ϊ�
- �f�J���g���W����ɍ��W�ցB���̃y�[�W�ł͋ɍ��W�ɂ��^���̋L�q�ɂ��čl�@���܂��B
- �ɍ��W���v���V�A��
- �f�J���g���W�ɂ�����2�����I�y���[�^�[���ɍ��W�ɕϊ������̂����x��3�����Ɋg�����Ă��̃I�y���[�^�[���ɍ��W�n�ɂ����Ăǂ̂悤�ɕ\���ł���̂����l�@���܂��B
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img68.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img69.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img70.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img71.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img72.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img73.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img74.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/coordinate_transformations_img2.png)
![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/sunset_glow_img1.jpg)















![���W�ϊ�,��]���W�n,�ɍ��W,��p�f,�͊w](./img/nida_img2.png)

