Dot Product
���ρ|Dot Product
�Q�̃x�N�g��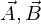 �̍��p��
�̍��p��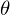 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A

��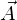 ��
��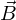 �̓��ςƂ�т܂��B
�̓��ςƂ�т܂��B
�ׂ��������̓e�L�X�g�ɔC���܂����A��{�x�N�g��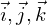 �͎��̌��������藧���܂��B
�͎��̌��������藧���܂��B
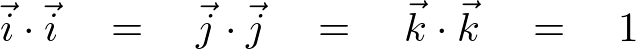
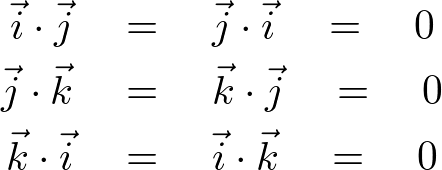
rotation�̃Z�N�V�����̖��ł͂��̌������g���Ă��܂��B
���Ȃ݂ɊO�ς�Cross Product�ƌ����Ă܂����A���ς̂ق���Dot Product�Ƃ�肵�܂��B
����
rotation�̌v�Z�ŏo�Ă��܂����݂Ƃ����L��������܂����B
����͕Δ�������Ƃ����L���Ń��E���h�ȂǂƌĂꂽ�肵�Ă��܂��B
���ɓ���l���邱�Ƃ͂Ȃ������P�ɕ���ɂ���ϐ��Ŕ�������A�Ƃ����Ӗ��ł��B
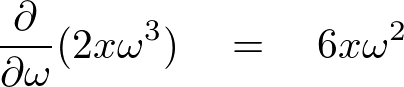
�Ƃ���ȋ�ł��B
�]�u�s��|transposed matrix
���ɓ���l����܂ł��Ȃ��s��v�f�̍s�Ɨ���i���ォ��E���ɑ���Ίp����Ɂj���ꊷ�����i�Ђ�����Ԃ����j�����ł��B
�Ⴆ�S�s�S��̍s��A
![�]�u�s��](../img/transposed_matrix_a_img2021_.png)
�́A�]�u����ƁA
![�]�u�s��](../img/transposed_matrix_a_img2021_2.png)
�ƂȂ�܂��B
���֘A�y�[�W
- ���`�㐔����
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �������p���`�㐔
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B


























